Nevlastní limita posloupnosti
Definice
Řekneme, že posloupnost \((a_n)\) má nevlastní limitu pokud buď
\(\forall K \in \mathbb{R} \quad \exists n_{0} \in \mathbb{N} \quad \forall n \gt n_0\) platí \(a_n \gt K\)
... nebo ...
\(\forall L \in \mathbb{R} \quad \exists n_{0} \in \mathbb{N} \quad \forall n \gt n_0\) platí \(a_n \lt L\)
Značení: \(\lim_{n \to +\infty} a_n = +\infty\) ... nebo ...
\(\lim_{n \to +\infty} a_n = -\infty\)

|
|

|
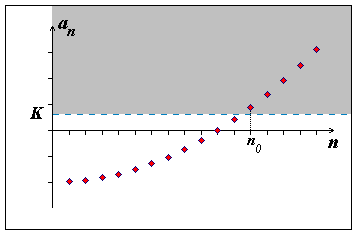
Obr. 5.2: Nevlastní limita \(+ \infty\)

|
|

|
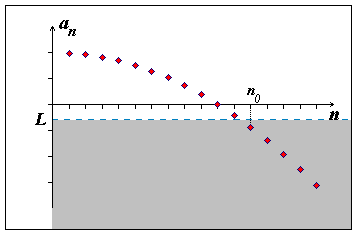
Obr. 5.3: Nevlastní limita \(- \infty\)
Pro každou posloupnost nastane právě jedna z následujících možností:
1. posloupnost má vlastní (reálnou) limitu \(\lim_{n o \infty} a_n = A\)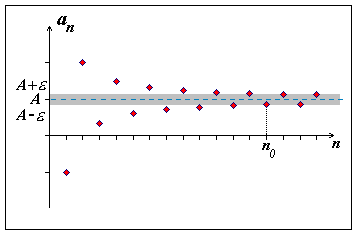
Obr. 5.3: Vlastní limita
2. posloupnost má nevlastní limitu \(\lim_{n o \infty} a_n = +\infty\)
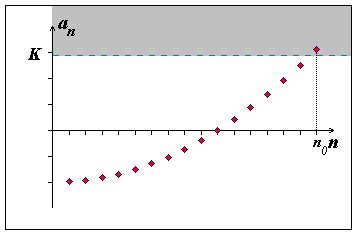
Obr. 5.4: Nevlastní limita
\(\lim_{n o \infty} a_n = -\infty\)
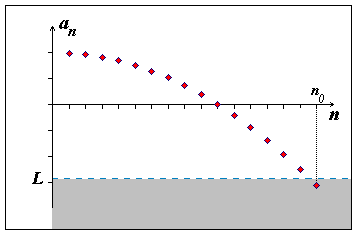
Obr. 5.5: Nevlastní limita
3. limita posloupnosti neexistuje
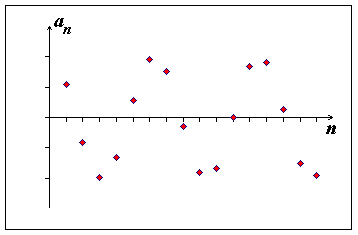
Obr. 5.6: Limita posloupnosti neexistuje
Limity speciálních posloupností
Aritmetická posloupnostNechť \((a_n)\) je aritmetická posloupnost s diferencí \(d\), potom ...
\(d = 0 \longrightarrow \) konvergentní 

\(d \not = 0 \longrightarrow \) divergentní 

Geometrická posloupnost
Nechť \((a_n)\) je geometrická posloupnost s kvocientem \(q\), potom ...
\(q \le -1 \longrightarrow \) divergentní
\(|q| \lt 1 \longrightarrow \) konvergentní, \(\lim a_n = 0\)
\(q = 1 \longrightarrow \) konvergentní
\(q \gt 1 \longrightarrow \) divergentní
Věta
Každá geometrická posloupnost \((a_n)_{n=1}^{\infty}\) pro jejíž kvocient \(q\) platí \(|q| \lt 1\) je konvergentní a \(\lim a_n = 0\)