Speciální posloupnosti
Různých druhů posloupností je mnoho. V této kapitole se blíže seznámíme se dvěma speciálními typy posloupností. Budou to aritmetické posloupnosti a geometrické posloupnosti.
Aritmetická posloupnost
Definice
Posloupnost \((a_n)\) se nazývá aritmetická právě tehdy, když
Číslo \(d\) se nazývá diference aritmetické posloupnosti.
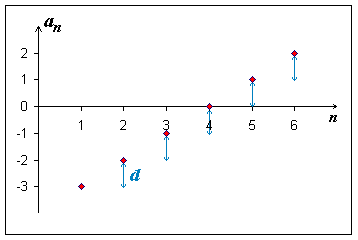
Posloupnosti jsou speciálním typem funkcí. Aritmetická posloupnost je "odvozená" od lineární funkce. Každou lineární funkci lze zapsat ve tvaru
\(y = k \cdot x + q\)
a každou aritmetickou posloupnost zase můžeme zapsat ve tvaru
\(a_n = d(n - 1) + a_1\)
\(a_n = d \cdot n + (a_1 - d)\)
... a to je právě tehdy, když každý člen posloupnosti (kromě prvního) je aritmetickým průměrem "svých sousedů".
\(\forall n \in N - \{1\}\) platí \(a_n = {{a_{n-1} + a_{n+1}} \over 2}\)

Vlastnosti aritmetických posloupností
monotónnost- rostoucí \(\Leftrightarrow d \gt 0\)
- klesající \(\Leftrightarrow d \lt 0\)
- shora omezená \(\Leftrightarrow d \lt 0\)
- zdola omezená \(\Leftrightarrow d \gt 0\)
- omezená \(\Leftrightarrow d = 0\)
Vztahy platící pro aritmetické posloupnosti
Věta
Nechť \((a_n)_{n=1}^{\infty}\) je aritmetická posloupnost s prvním členem \(a_1\) a diferencí \(d\), potom platí\(a_n = a_1 + (n-1)d\)
Věta
Nechť \((a_n)_{n=1}^{\infty}\) je aritmetická posloupnost s prvním členem \(a_1\) a diferencí \(d\), potom pro součet \(s_n\), prvních \(n\) členů této aritmetické posloupnosti platí\(s_n = {n \over 2} (a_1 + a_n)\)